Pareto snakes and Markov ladders

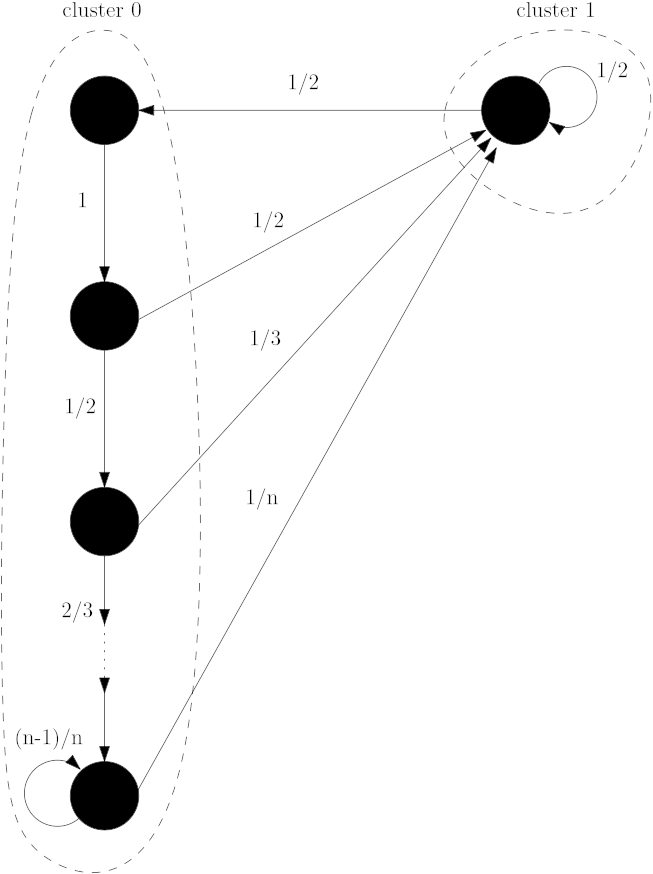
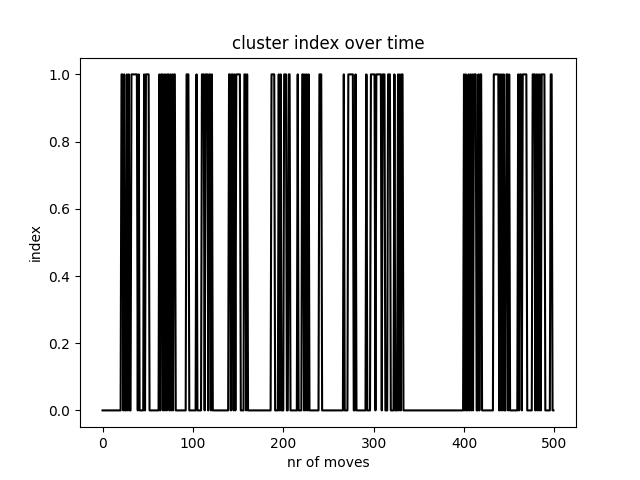
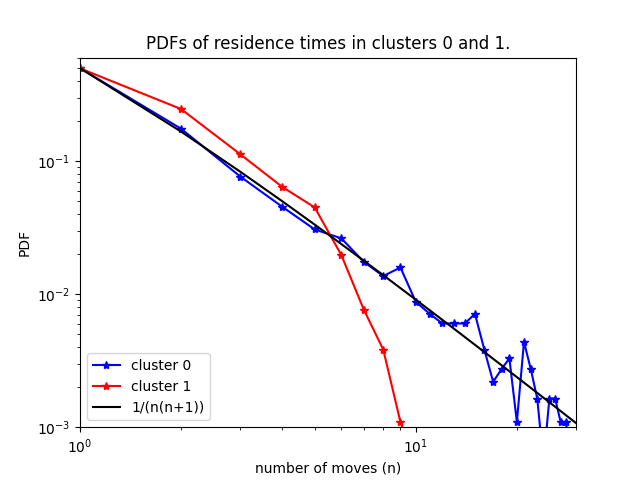
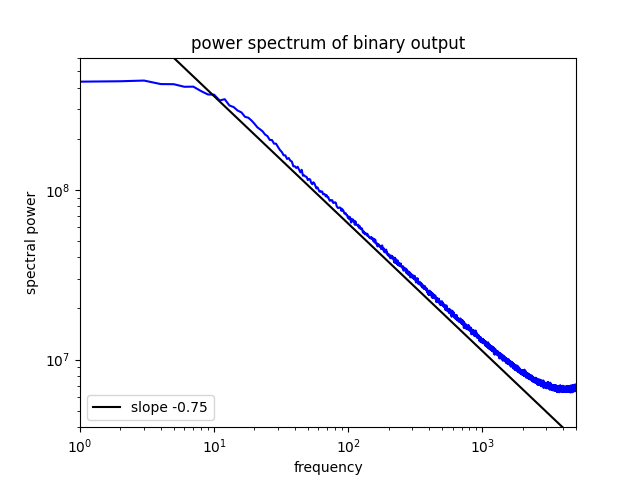
A question that has been on my mind for a while now is how Markovian dynamics can give rise to "flickering noise", i.e. a power spectrum with (a range of) 1/f like behaviour. Below is an example, loosely based on the game of "snakes and ladders". Let the output signal be 0 when the state is in cluster 0 and 1 if it is in cluster 1. A simple computation shows that the probability of residence times is algebraic for cluster 0 and exponential for cluster 1. Thus, the spectrum is that of an alternating fractal renewal process (see Lowen & Teich's Fractal-based point processes). Shown are the averaged results of 4,000 simulations with 200 "ladders". The truncation of the chain in cluster 0 leads to a truncation of the range in which flickering noise is observed.

Of course, this example is not very satisfactory because the algebraic decay of the probability distribution is caused by the hard-coded algebraic decay of the weights coupling the clusters. I have since had better ideas...